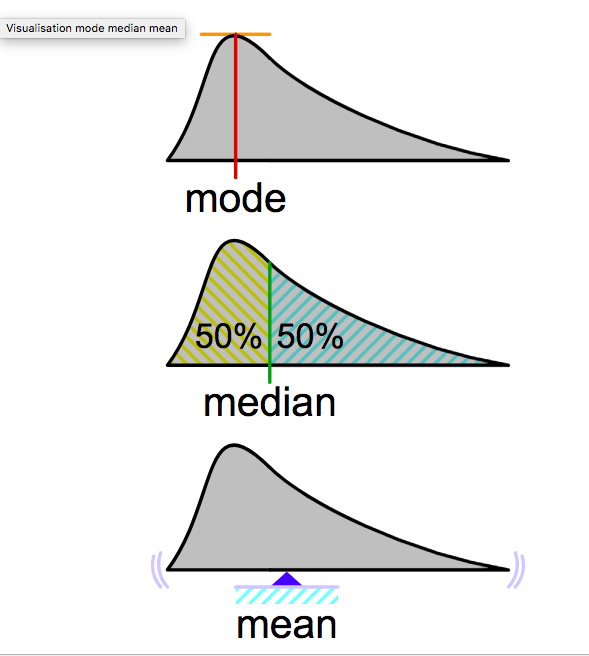
median mode and mean for continuous probability density function

In discrete case, finding mean is easy.
finding mode is equivalent to finding a number that has most occurences in an array.
For example: a = [4,2,3,4,5,6,9,4,2,1,4,8,7], we can use a hashtable and scan every number in the array, which runs in O(n)
finding median is hard when I first thought about it. The first solution I thought was sort the array first, which can be done at the best case of O(nlogn). And find the middle index. If arrayy is odd, the it’s (1+length(a))/2, and if it’s even, it’s the average of two numbers in the middle.
But on CS61B lecture slide, it can be done in O(n).
This problem is equivalent to finding a number that half the numbers greater than it and half the numbers less than it.
I DON’T KNOW IT YET. I will think it later.

In continuous case, mean is the definitoin of E(x). Just the integral. Mode is the x corresponding to the hightest y. Use derivative to find the maximum. Median is the half point. Make the integral to 1/2, and finding the x.